Understanding Non-uniform Forces in the Throws with Implications
for Training
by
Wayne T. Armbrust, Ph.D.
Submitted in Partial Fulfillment of the Requirements for USA Track
and Field Coaching Education Level III designation
I. Introduction
This paper, part of the requirement for Level III designation in the
USA Track and Field Coaching Education program focuses on an area usually
neglected in studies of the throwing events. Starting from basic kinematic
and dynamic considerations involving non-uniform forces, we relate work done
on an implement to the distance thrown, and graphically illustrate areas
where specific training methods are likely to improve results.
II. Projectile Motion
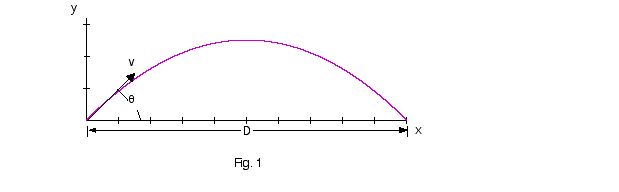
We consider a projectile moving with an initial velocity v making
an initial angle of ø with the ground. This will approximate an
implement thrown with a velocity of release v and angle of release ø
( Fig. 1). We neglect considerations of air resistance, aerodynamic effects,
and height of release, since to first order approximation these considerations
will not effect our conclusions. Since distances traveled by thrown implements
are small compared with the size of the earth, no error is introduced by
assuming the acceleration due to gravity to be constant and neglecting effects
of the curvature of the earth. From elementary physics8 it is
easy to show that D, the distance traveled by a projectile under these assumptions
is given by
D = (v2/g)sin(2ø).
(Eq. 1)
where g is the acceleration due to gravity.
From Eq. 1 we see that sin(2ø) equals 1 when ø equals 45°,
hence the maximum distance is achieved at this angle of release. This
result is true only under the assumption of no air resistance or aerodynamic
effects and not considering the height of release. It also assumes that
the velocity of release is independent of the angle of release, which is
not strictly true for a thrower. Air resistance, aerodynamic effects, and
height of release all have the effect of making the optimal angle of release
less than 45°, as does the fact that greater force can in general be
generated at smaller angles of release. None of these considerations will
effect the conclusions we are about to develop, however, since for a particular
implement and athlete there will an optimal angle of release, øm, which will result in the maximum distance,
Dm. Dm
is given by
Dm = (v2/g)sin(2øm). (Eq. 2)
III. Work and Kinetic Energy
A. Uniform Forces For a body starting from rest and accelerating
at a constant rate, the kinematic relationship between velocity, acceleration,
and distance is give by
v2 = 2as, (Eq. 3)
where a is the acceleration and s is the distance over which the acceleration
occurs.
For a constant force, Work , W, is defined as
W = Fs. (Eq. 4)
Substitution of Newton’s Second Law (F = ma) in Eq. 3 gives
us
Fs = W = (1/2)mv2. (Eq.
5)
Here we follow the normal convention of representing vectors, quantities
having direction as well as magnitude, in bold face.
The quantity (1/2)mv2 is defined as the
kinetic energy. of an object. Eq. 5 expresses the very import
relationship between work and kinetic energy; if an object starts from
rest, it will have a final kinetic energy equal to the work done on it.
Work in the case of a constant force F acting through a distance s
is graphically represented in Fig. 2 by the shaded rectangular area.
If we compare Eqs. 2 and 5 we obtain the result
Dm = (2W/mg)sin(2øm). (Eq. 6)
Thus, the distance an implement is thrown is directly proportional
to the work done on the implement. No doubt many readers will
have heard that distance thrown is proportional to the product of force
and the distance through which the force acts. The derivation above is
the origin of this statement, but is exact only for constant force.

B. Non-uniform Forces In nature, few forces are ever constant.
This is especially true in track and field and the throws in particular.
For a non-uniform force that varies in both magnitude and direction,
the differential element of work is defined as
dW = F . ds
= (Fcosø)ds (Eq. 7)
where F is the instantaneous force, ds is the differential
element of displacement, and ø is the angle between F and
ds. ds is always tangent to the displacement curve, which
can be of arbitrary shape. Likewise, F can constantly change in
direction and
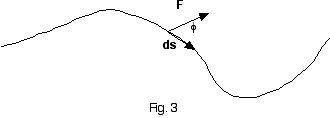
magnitude. ø, the angle between the F and ds can
also constantly change. A differential element of work is illustrated in
Fig. 3. The differential work elements are integrated over the total displacement
to calculate the total work.
A typical plot of Fcosø vs. s for a throwing event is shown
in Fig. 4. Force, initially zero, builds to a maximum at an intermediate
point and then decreases until release. The relationship between work and
the area under the force vs. displacement curve from the previous section
can be generalized to the case of non-uniform forces. For non-uniform forces,
work is also the area under the Fcosø vs. s curve. Thus, we arrive
a very important result: Increased throwing distances are equivalent
to increased area under the Fcosø vs. s curve.
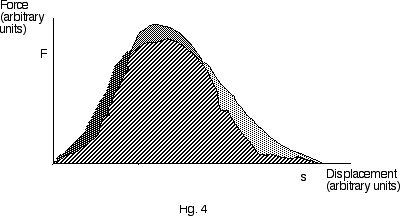
IV. Implications
Having developed the relationship between work done on an implement
and distance of the throw, we seek ways of increasing the area under the
curve in Fig. 4. We will consider the area shaded

to correspond to the work produced on the implement by the thrower,
and hence proportional to the resulting distance, employing a base level
of training. We now explore ways in which to increase the area under the
curve in Fig. 4 beyond the base level.
Consider the portion on top of the curve shaded
 .
.
We may think of this portion of the curve as resulting from improvement
to peak force developed by the athlete. Peak force training is
the most common type of strength training undertaken by throwers, and typically
consists of training such as 1-3 sets of 3-5 repetitions of appropriate
lifts at 75-95% SRM performed at relatively low speed12. Bompa1
recommends a maximum strength phase prior to training at a sport-specific
combination of strength and speed. Unfortunately, many throwers, even
those performing at a relatively high level, limit themselves by not going
beyond this phase in their training. At this point we should note that
the peak force developed in the throw will be less than the maximum force
of which the athlete is capable. This is because the implement is moving
at this point and it is well-known that the force of muscular contraction
is inversely proportional to the speed of muscular contraction6.
The force-velocity curve is illustrated in Fig. 5. Therefore, specific
training for peak force in the throws should include training at moderate
force - moderate speed of contraction4. Typical training of this
type includes snatch and release or press and release exercises with moderate
weight. Conventional training emphasizes only the left portion of the
curve, i.e., large forces and low speeds.
Next let us consider the portion of the curve shaded

at the initiation of the throw. This represents the increase in
area under the force vs. displacement curve realized by increasing
the initial slope of the curve, the rate of force development.
Training to improve rate of force development should obviously be part
of every thrower’s training program. If the total area under the force
vs. displacement curve can be increased by even a few percent through
improvement in this part of the curve, distance will correspondingly increase.
Methods employed to improve rate of force development involve explosive,
ballistic movements with moderate to heavy resistance, seeking to accelerate
the weight as quickly as possible7,9,10, and plyometric training2.
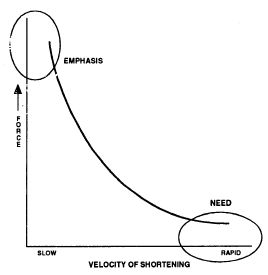
Fig. 54
Finally we consider the right hand portion of the force vs. displacement
curve in Fig. 4. This portion of the curve is characterized by a high
rate of muscular contraction since it occurs just prior to release
of the implement. Decrease of force with velocity, while retaining an
inverse relationship, can be reduced through appropriate training. Training
in the right hand portion of the curve of Fig. 5 will improve applied force
at high speed4 and increase the area under the curve on the right
hand portion of Fig 4. Specific training to increase force at high rates
of muscular contraction include medicine ball and power ball drills5
and other high speed, low intensity resistance training13.
Plyometrics are also shown to improve force production at high velocities3.
The portion of the curve in Fig. 4 shaded

illustrates improvement as a result of this type of training.
V. Conclusions
We have derived the relationship between the work done on an implement
and the distance thrown, and have shown that to increase distance we must
increase the area under the force vs. displacement curve. Those
portions of the force vs. displacement curve where enhancement is
most likely include increasing the rate of force development at the beginning
of the throw and increasing force at high rates of muscular contraction before
the release. Specific training suggestions for improvement in these areas
include explosive, ballistic resistance training, high speed, low resistance
exercises such as medicine ball training, and plyometrics.
VI. References
1. Bompa, T. O., Theory and Methodology of Training: The Key to Athletic
Performance, 3rd Ed, Debuque: Kendall/Hunt Publishing Company,
1994.
2. Chu, D.A., Jumping into Plyometrics, Human Kinetics, Champaign,
IL, 1991
3. Chu, D. (1983), Plyometrics: The Link Between Strength and Speed,
National
Strength and Conditioning Association Journal, 5(2):20-21.
4. Gambetta, V. (1987), How Much Strength is Enough? National
Strength and
Conditioning Journal, 9(3):51-53.
5. Gambetta, V., and Odgers, S., The Complete Guide to Medicine
Ball
Training, Sarasota, Florida: Optimum Sports Training, 1991.
6. Hill, A. V. (1953), The Mechanics of Active Muscle, Proc Roy
Soc Lond (Biol),
141:104-117.
7. Newton, R. & Kraemer, W. (1994), Developing Explosive Muscular
Power:
Implications for a Mixed Training Strategy, Strength and Conditioning,
16(5):20-31.
8. Resnick, R. & Halliday, D., Physics for Students of Science
and
Engineering, New York: John Wiley & Sons, Inc., 1960.
9. Sale, D.G. (1988), Neural adaptations to resistance training, Medicine
and
Science in Sport and Exercise, 20:S135-S245.
10. Schmidbleicher, D. (1985), Strength Training Part I: Classification
of Methods,
Sports Science Periodical on Research and Technology in Sport,
August 1985:1–12.
11. Siff, M. C. and Verkhoshansky, Y. V., Supertraining, Pittsburgh:
Sports Science
Syndicate, 1996.
12. Stone, M., and O’Bryant, H., Weight Training: A Scientific
Approach,
Minneapolis, Minnesota: Burgess Publishing Company, 1987.
13. Zatsiorsky, V. M., Science and Practice of Strength Training,
Human
Kinetics, Champaign, IL, 1995.
#





 .
.

